Calculating Hull Speed & The Speed/Length Ratio
In a Nutshell
Hull speed's a theoretical top speed for a displacement boat, and it's mostly determined by its waterline length. You can figure it out by taking the square root of the waterline length in feet and multiplying it by a constant, 1.34.
This formula's a great guideline, but it's really just the point where resistance starts to get serious. Modern designs, especially those with fine bows or the ability to plane, can actually go a lot faster. For a sailor, understanding hull speed is really about knowing what you can realistically expect from your boat.
Table of Contents
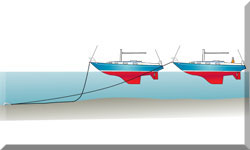
 A light-displacement hull like this one will have less hull drag than a heavy displacement hull as a result of its lower wetted area
A light-displacement hull like this one will have less hull drag than a heavy displacement hull as a result of its lower wetted areaWhat is Hull Speed & How is it Calculated?
Sailors and engineers have always been fascinated by what makes one boat faster than another. It was a British engineer named William Froude (1810-1869) who gave us the scientific answer. Through tank testing and model analysis, Froude proved there's a basic relationship between a boat's speed and its waterline length, a relationship described in the metric world by the 'Froude Number'.
Most of us in the imperial world of feet and knots are probably more familiar with its close relative—the Speed/Length Ratio. This simple formula lets you compare the performance of boats of different lengths by normalising their speeds to their waterline length.
The Speed/Length Ratio = hullspeed (in knots) divided by the square root of the waterline length (in feet).
A sailboat moving at a speed/length ratio of 1.34 is considered to be at its theoretical hull speed. This is the point at which the boat's own bow and stern waves begin to create a 'wave train' that traps the hull. To go faster, the boat must overcome this resistance, a process that requires a disproportionate increase in power.
Why are There Different Kinds of Hull Resistance?
A sailboat's trip through the water is a constant fight against resistance. It's really caused by two main factors: frictional resistance and wave-making resistance.
- Frictional Resistance: This is the drag caused by water moving over the hull’s wetted surface area. It's a lot like dragging your hand across a rough surface—the friction comes from the water's viscosity and the hull's smoothness. A dirty hull with barnacles or weed growth really increases this resistance. A clean, smooth hull is one of the most important things you can do to reduce frictional drag. I've seen at firsthand how a boat that was sluggish suddenly comes alive after a quick scrub of the hull.
- Wave-Making Resistance: As your boat moves, it creates waves. At slow speeds, they're small and harmless. But as you get faster, the waves get bigger. Once you hit hull speed, the wavelength becomes equal to your boat's waterline length. The bow sits in the trough of its own wave, and the stern sits in the trough of another, creating a barrier that's really hard to climb over.
The total resistance of a hull is the combination of these two things. At slower speeds, frictional resistance is the big problem, but at higher speeds, wave-making resistance takes over.
Is the 'Hull Speed' a True Limit?
That 1.34 constant is a good rule of thumb, but it's not a law you can't break. It's most accurate for traditional, heavy-displacement hulls. Modern boat design has definitely challenged, and in some cases, shattered this idea.
- Planing Hulls: Many modern racing yachts, especially with wide, flat sterns, are designed to transition from a displacement boat to a planing one. With enough power from the sails, the hull can lift out of its own bow wave and skim across the water's surface. This dramatically reduces wave-making resistance and lets it go much faster than its theoretical hull speed.
- Multihulls: Catamarans and trimarans are designed to avoid the hull speed trap altogether. Their long, skinny hulls have a really high Speed/Length ratio and create very little wave-making resistance. They don't get "stuck" in a wave train and can therefore achieve much higher speeds than a monohull of the same length.
For a cruising sailor, the 1.34 rule is a solid benchmark for understanding what you can realistically expect from your boat's performance in normal conditions.
Beyond Hull Length: Other Factors Affecting Speed
While hull length is the main thing that determines a boat's theoretical speed, there are other factors that matter for its overall performance.
- Displacement: A lighter boat needs less energy to push through the water because it displaces less water and creates smaller waves.
- Wetted Surface Area: The more of the hull, keel, and rudder that's in contact with the water, the more frictional drag there is. Keel design is a delicate balance of providing enough lateral resistance to prevent leeway while keeping wetted area to a minimum.
- Hull Shape & Fairing: The shape of the hull at the bow and stern has a big impact on wave-making resistance. Fine, narrow bows can cut through the water more cleanly than full, blunt ones. A smooth, well-faired hull helps the water flow more efficiently over the surface, which reduces drag.
- Keel & Rudder Balance: The relationship between your sail plan's center of effort and your hull’s center of lateral resistance is really important for steering. A well-balanced boat with a slight "weather helm"—a tendency to turn into the wind—is both safer and faster. Too much weather helm forces you to turn the rudder too much, which just creates drag and slows you down.
Propeller Drag & Its Effect on Speed
For any sailboat with an auxiliary engine, the propeller can be a significant source of drag, acting like a brake when you're under sail. This phenomenon, known as propeller drag, is especially noticeable on light, performance-oriented vessels.
The physics behind it is pretty simple. When the engine's off and you're sailing, a fixed-blade propeller acts like a stalled foil. As water rushes over the blades, it creates turbulence and resistance, acting like a tiny paddle wheel being dragged through the water. This extra drag can slow a sailboat down by a significant amount, sometimes as much as 1 knot.
To fix this, sailors often go for different propeller designs:
- Folding Propellers: These propellers have hinged blades that fold back against the hub when the shaft isn't turning. This reduces the wetted area and gets rid of the draggy shape of the blades, making for a much more streamlined profile.
- Feathering Propellers: These are more complicated, with blades that can pivot to line up with the flow of water when they're not in use. This "feathered" position creates minimal resistance and also works well for going forward or in reverse.
For a sailor who cares about performance, whether they're racing or cruising long distances, the propeller you choose is a critical decision. Cutting down on that passive drag lets your boat perform closer to its theoretical speed potential and improves its overall efficiency.
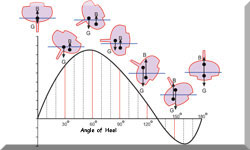
Heel & Its Impact on Waterline Length
When a monohull sails, it heels over, changing its effective waterline length. For many modern racing designs, this can actually increase the waterline length, allowing the boat to reach higher speeds. It's a fascinating counterintuitive concept to explain—that heeling, which seems to add resistance, can actually be part of a sailboat's design to increase performance.
| Waterline Length | Max Hull Speed |
|---|---|
| 20 feet | 6.0 knots |
| 25 feet | 6.7 knots |
| 30 feet | 7.3 knots |
| 35 feet | 7.9 knots |
| 40 feet | 8.5 knots |
| 45 feet | 9.0 knots |
| 50 feet | 9.5 knots |
Practical Considerations: Sea State & Currents
The theoretical calculations of hull speed assume calm, flat water. In reality, a sailboat's speed is a product of its performance through the water (STW) and the external forces acting on it, such as waves and currents. For an offshore sailor, understanding these variables is as important as knowing your boat's theoretical limits.
The Influence of Sea State
The state of the sea has a big impact on a boat's speed and efficiency. A boat sailing in a head sea—with waves coming right at the bow—will definitely slow down as the hull's forced to push up and over each wave. This repeated motion, called pitching, messes up the flow over the hull and makes it hard to keep your speed up. On the other hand, a boat riding a following sea can actually gain speed. The energy from the waves can help push the boat forward, letting it surf and temporarily go faster than its theoretical hull speed. When you're in a beam sea, a boat's motion becomes an uncomfortable roll, which can also reduce your speed.
Speed Through the Water vs. Speed Over the Ground
While your knotmeter tells you your speed through the water (STW), your GPS gives you your speed over the ground (SOG). The difference between the two is the effect of the current. A favorable current adds to your SOG, pushing you toward your destination faster than your STW might suggest. An opposing current, though, subtracts from your SOG, forcing you to use more time or energy to cover the same distance. For smart navigation and passage planning, you've always got to consider how currents affect your SOG.
When it comes to understanding sailboat design, factors like hull shape and ratios are critical. For a more comprehensive look at these topics and their impact on your vessel's performance and safety, be sure to read our full guide, "Mastering Sailboat Design Ratios & Regulation for Performance & Safety."
This article was written by Dick McClary, RYA Yachtmaster and author of the RYA publications 'Offshore Sailing' and 'Fishing Afloat', member of The Yachting Journalists Association (YJA), and erstwhile member of the Ocean Cruising Club (OCC).
FAQs
Can a sailboat ever go faster than its hull speed?
Can a sailboat ever go faster than its hull speed?
Yes, while the 1.34 constant is a rule of thumb for displacement hulls, modern designs like catamarans or monohulls with planing capabilities can and do exceed this speed, often by a significant margin.
Does adding a more powerful engine to a displacement hull increase its top speed?
Does adding a more powerful engine to a displacement hull increase its top speed?
No. A displacement hull is limited by its physics. Adding more power simply creates larger, steeper waves without a meaningful increase in speed.
How does a long, narrow hull compare to a short, wide one?
How does a long, narrow hull compare to a short, wide one?
A longer waterline length allows for a higher theoretical hull speed. A long, narrow hull will typically have less wave-making resistance and be more efficient at speed than a short, wide hull of the same displacement.
Resources Used
- SailZing: https://sailzing.com/hull-smoothness-what-matters-for-speed/
- Cox Marine: https://coxmarine.com/blog/what-affects-boat-speed-2/
- Yachting Monthly: https://www.yachtingmonthly.com/sailing-skills/busting-the-hull-speed-myth-82832
- Neural Concept: https://www.neuralconcept.com/post/full-guide-to-hydrodynamic-simulation-theory-to-application
- Wikipedia: https://en.wikipedia.org/wiki/Froude_number
Recent Articles
-
Ohlson 38 Guide: Specs, Performance Analysis & Cruising Review
Jan 07, 26 05:52 AM
Discover the Ohlson 38 sailboat. An in-depth look at its Einar Ohlson design, Tyler GRP construction, performance ratios, and why it remains a top choice for offshore sailors. -
Passoa 47 Sailboat Review: Comprehensive Specs & Performance Analysis
Jan 04, 26 04:57 AM
Discover the Passoa 47, a legendary aluminium blue water cruiser by Garcia. Explore technical specifications, design ratios, and why its lifting keel is a game-changer for offshore sailors. -
Sailboat Wheel Steering Maintenance & Inspection Checklist
Dec 30, 25 02:32 PM
Keep your vessel’s helm responsive and reliable with our expert maintenance checklist. Master cable tensioning and system inspections to avoid mid-passage failures.